はじめに
こんにちは、ぱるまです。ABC334 B がなかなか難しかったのですが、いろいろ学びが得られたので、備忘録として記事を書きます。
この記事では、競プロでよく現れそうないくつかの思考パターンと、その思考パターンを使った ABC334 B の解法をいくつか書いていきます。 具体的には、以下の思考パターンを使います。
- 簡単な問題を作って考える
- 答えが変わらない範囲で値を都合よく動かす
- 閉区間を半開区間にして考える
- $g([a, b)) = f(b) - f(a)$ の形にできないか検討する
- 負が扱いにくいならば正の領域に平行移動する
- 正負の対称性を考える
問題の概要
ABC334 B (Christmas Trees) の問題を簡潔に書くと以下のようになります。
$M, A, L, R \in \mathbb{Z}, M \geq 1$ のときに、$(M\mathbb{Z} + A) \cap [L, R]$ の要素数を求めてください。
制約:
- $-10^{18} \leq A \leq 10^{18}$
- $1 \leq M \leq 10^{9}$
- $-10^{18} \leq L \leq R \leq 10^{18}$
ただし、$M\mathbb{Z} + A := \{Mx + A \mid x \in \mathbb{Z}\}$, $[L, R] := \{x\in \mathbb{Z} \mid L \leq x \leq R\}$ とします。
ここでは、簡単のため $A = 0$ とします。 (全体的に $-A$ 平行移動して、$(A, L, R)$ を $(0, L-A, R-A)$ に置き換えて考えることで、$A=0$ の問題に帰着できます)
つまり、以下の問題を考えます。
$M, L, R \in \mathbb{Z}, M \geq 1$ のときに、 $(M\mathbb{Z}) \cap [L, R]$ の要素数を求めてください
簡単な問題を作って考える
難しい問題に対しては、簡単な問題を作って考えてみるというのが有効です。 今回の問題でいうと、簡単な問題として例えば以下のものが挙げられます。
- $L=0$, $R>0$ の場合
- $\lfloor R/M\rfloor + 1$ が答えです
- $L>0$, $R>0$ の場合
- 後述します
- $L$ と $R$ が $M_{}$ の倍数の場合
- $(R - L)/M + 1$ が答えです
- etc.
($A=0$ とするのも「簡単な問題にする」と言えそうです。この記事では最初から $A=0$ としてしまっています)
以降は、これらのような「簡単な問題」をベースに解法を考えていきます。
答えが変わらない範囲で値を都合よく動かす
$L$ と $R$ が $M_{}$ の倍数であれば、答えは $(R - L)/M + 1$ であることはすぐにわかります(植木算)。$L$ と $R$ が $M_{}$ の倍数とは限らない点がこの問題の難しいところです。
「答えが変わらない範囲で値を都合よく動かす」というのをすると、$L$ と $R$ が $M_{}$ の倍数の場合に帰着させることができます。
例えば、
- $L'$ を $L$ 以上の $M_{}$ の倍数で最小の整数($M_{}$ の倍数への切り上げ)
- $R'$ を $R$ 以下の $M_{}$ の倍数で最大の整数($M_{}$ の倍数への切り捨て)
とします。このとき、$(M\mathbb{Z}) \cap [L, R] = (M\mathbb{Z}) \cap [L', R']$ となります(以下の図を参照してください)。
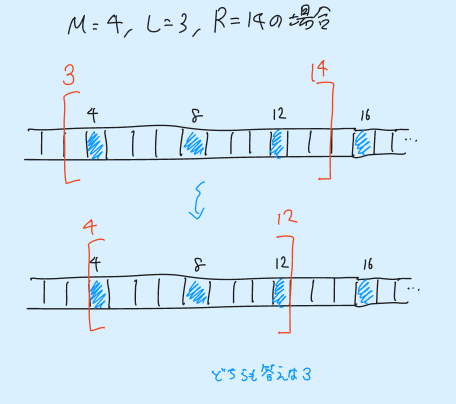
$L'$ と $R'$ は
- $L' = \lceil L/M \rceil M_{}$
- $R' = \lfloor R/M \rfloor M_{}$
なので、求めたい要素数は $(R' - L')/M + 1 = \lfloor R/M \rfloor - \lceil L/M \rceil + 1$ と求まります。
なお、この解法はごりさんの以下の記事と本質的に同じ解法です。こちらも合わせてご覧ください。
閉区間を半開区間にして考える
競プロでは、閉区間($[a,b]$ という形)で考えるより、半開区間($[a, b)$ という形)で考えるほうがいいことが多いがちです(累積和などがそう)。
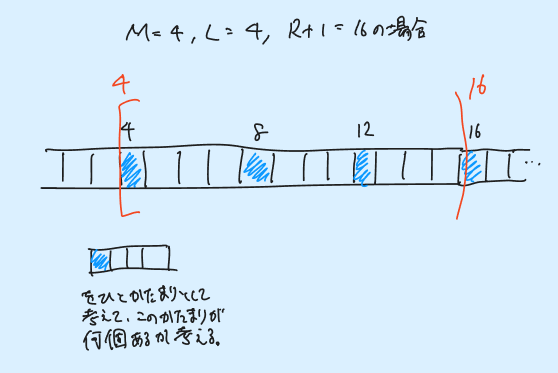
ここでは、$[L, R] = [L, R+1)$ として考えてみます。 まずは、$L$ と $R+1$ が $M_{}$ の倍数であるという「簡単な問題」を考えます。 以下の図のように考えることで答えは $(R + 1 - L)/M_{}$ であることがわかります。
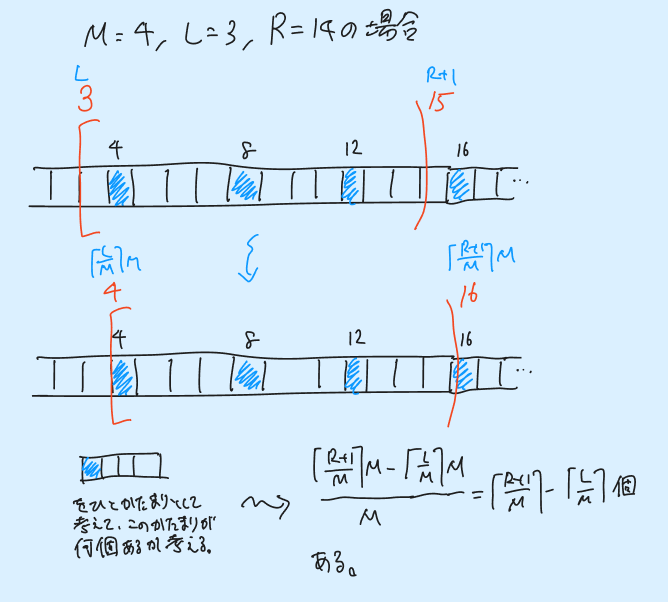
次に、$L$ と $R+1$ が $M_{}$ の倍数とは限らない場合を考えます。 先程の「答えが変わらない範囲で値を都合よく動かす」を行い、$L$ と $R+1$ を $M_{}$ の倍数に切り上げすることで、$L$ と $R+1$ が $M_{}$ の倍数の場合に帰着させることができます。 以下の図のように考えることで $\lceil (R+1)/M\rceil - \lceil L/M\rceil$ という答えが得られます。
なお、$[a,b)$ という半開区間ではなく、$(a, b]$ という半開区間で考えても同様に求められます。 その場合は、$\lfloor R/M\rfloor - \lfloor (L - 1)/M\rfloor$ という形で答えが出てきます。
$g([a, b)) = f(b) - f(a)$ の形にできないか検討する
$g([a, b)) = f(b) - f(a)$ という形の変形はたまに出てきます(代表例は累積和)。こういう式変形ができないか検討します。
$L>0$, $R>0$ の場合で考えます。 有限集合 $S \subseteq \mathbb{Z}$ に対して、$g(S) =|(M\mathbb{Z}) \cap S|$ とします。求めたいものは $g([L, R])$ です。
$S_1\subseteq S_2$ のとき、$g(S_2\setminus S_1) = g(S_2)- g(S_1)$ が成り立ちます。よって、以下のように変形できます。
$$ \begin{align} g([L, R]) &= g([L, R + 1))\\ &= g([0, R+1) \setminus [0, L))\\ &= g([0, R+1)) - g([0, L))\\ \end{align} $$
ここで、$f(x) := g([0, x))$ を求めればよいのですが、$f(x) = \lceil x/M\rceil$ と求まります。
ゆえに答えは $g([L, R]) = \lceil (R+1)/M\rceil - \lceil L/M\rceil$ と求まります。
日本語で書くと: $[L,R] = [L, R+1)$ の区間での $M_{}$ の倍数の個数は、
としたとき、$C_2 - C_1$ で求められる、ということです。
補足1: $(L - 1, R]$ という半開区間を考える
今回の問題は、$[L, R] = [L, R + 1)$ とするより、$[L,R] = (L - 1, R]$ としてもよいです(結果論としてそのほうがわかりやすい)
以下のように式変形できます。 $$ \begin{align} g([L, R]) &= g(_{}(L - 1, R])\\ &= g(_{}(0, R] \setminus (0, L - 1])\\ &= g(_{}(0, R]) - g(_{}(0, L - 1]) \end{align} $$ $f(x) := g(_{}(0, x])$ を求めればよいのですが、$f(x) = \lfloor x/M\rfloor$ と求まります。(ceil より floor のほうが簡単がち)
ゆえに $g([L, R]) = \lfloor R/M\rfloor - \lfloor (L - 1)/M\rfloor$ と求まります。
補足2: $L, R$ が負の場合
$L, R$ が負の場合は 0の代わりに小さな負の数を考えるか、後述のように正の領域に平行移動するとよいです。
「0の代わりに小さな負の数を考える」方針は例えば以下のようになります。
十分小さな $M_{}$ の倍数 $kM_{}$ を取ります($kM \le L$ を満たしているとします)。
\begin{align} g([L, R]) &= g(_{}(L - 1, R])\\ &= g(_{}(kM, R] \setminus (kM, L - 1])\\ &= g(_{}(kM, R]) - g(_{}(kM, L - 1]) \end{align}
ここで、$x> kM_{}$ に対して $g(_{}(kM, x]) = \lfloor (x-kM)/M \rfloor = \lfloor x/M\rfloor - k$ なので、 $g([L, R]) = \lfloor R/M\rfloor - \lfloor (L - 1)/M\rfloor$ と求まります。($k$ が打ち消しあう)
負が扱いにくいならば正の領域に平行移動する
$L$ や $R$ が負だと考えづらいので、$L$ や $R$ を正の領域に動かして考えます。これも「答えが変わらない範囲で値を都合よく動かす」と言えます。
$x$ が $M_{}$ の倍数のとき、$|(M\mathbb{Z}) \cap [L, R]| = |(M\mathbb{Z}) \cap [L + x, R + x]|$ が言えます。つまり、$x$ が $M_{}$ の倍数のとき、$[L, R]$ を $x$ だけ平行移動しても答えは変わらないということです。($x$ が $M_{}$ の倍数でない場合はそうとは限らないので注意です。)
そこで、$k\in \mathbb{Z}$ を十分大きく取り、$kM_{}$ だけ平行移動してみます。
つまり、
- $L' = L + kM_{}$
- $R' = R + kM_{}$
とし、$L', R' > 0$ となるように $k$ が取られているとします。
$|(M\mathbb{Z}) \cap [L, R]| = |(M\mathbb{Z}) \cap [L', R']|$ なので、$L, R > 0$ の場合に帰着できました。
$\lfloor (R + kM)/M\rfloor = \lfloor R/M\rfloor + k$ のように計算することで、 \begin{align} |(M\mathbb{Z}) \cap [L', R']| &= \lfloor R'/M\rfloor - \lfloor (L'-1)/M\rfloor \\ &= \lfloor (R + kM)/M\rfloor - \lfloor (L + kM -1)/M\rfloor \\ &= (\lfloor R/M\rfloor + k) - (\lfloor (L -1)/M\rfloor + k) \\ &= \lfloor R/M\rfloor - \lfloor (L - 1)/M\rfloor \end{align} と求まります
正負の対称性を考える
「簡単な問題」として、$x > 0$ の場合に $|{M\mathbb{Z}}\cap (0, x]|$ を求める問題から考えたとします。
- $f(x) = \lfloor x/M\rfloor$ とします。$x>0$ のとき $|{M\mathbb{Z}}\cap (0, x]| =f(x)$ と求まります。
- 正負の対称性から、$x<0$ のとき $|{M\mathbb{Z}}\cap [x, 0)|=f(-x)$ と求まります。
$|{M\mathbb{Z}}\cap (0, x]| = f(x)$ と $|{M\mathbb{Z}}\cap [x, 0)| = f(-x)$ を組み合わせることで、$|{M\mathbb{Z}}\cap [L, R]|$ は以下のように解けます。
- $L > 0 , R > 0$ の場合:
- $[L,R] = (0, R] \setminus (0, L - 1]$ と考えることで、$f(R) - f(L - 1)$ と求まります。
- $L \leq 0, R\geq 0$ の場合:
- $[L,R] = [L, 0) \cup \{0\} \cup (0, R]$ と考えることで、$f(-L) + 1 + f(R)$ と求まります。
- $L <0, R <0$ の場合:
- $[L,R] = [L, 0) \setminus [R + 1, 0)$ と考えることで、$f(-L) - f(-(R+1))$ が答えです。
- または、正負の対称性から $(L, R)$ を $(-R, -L)$ と改めて正の場合に帰着させても良さそうです。
(コンテスト中はこれに近い解法で解きました。)
おわりに
競プロでよく現れそうないくつかの思考パターンを使って、ABC334 B の解法をいくつか書いていきました。具体的には以下の思考パターンを使いました
- 簡単な問題を作って考える
- 答えが変わらない範囲で値を都合よく動かす
- 閉区間を半開区間にして考える
- $g([a, b)) = f(b) - f(a)$ の形にできないか検討する
- 負が扱いにくいならば正の領域に平行移動する
- 正負の対称性を考える
ABC334 B はめっちゃ難しくてコンテスト中は苦戦しましたが、いろいろな競プロの思考法を整理するきっかけになってよかったです。